Multi-Layer Perceptrons

Multi-Layer Perceptrons (MLPs) have garnered considerable attention among the various neural network types. This is primarily due to their capacity to effectively manage non-linear relationships and excel in tasks encompassing pattern recognition, classification, and regression. In this segment, we delve into the complexities of MLPs, exploring their architecture, training algorithms, and their applications within the realm of artificial intelligence.

Multi-Layer Perceptrons consist of multiple layers of interconnected perceptrons, as discussed in the preceding section. Unlike single-layer perceptrons, which are limited to addressing linearly separable problems, Multi-Layer Perceptrons can tackle more intricate tasks by incorporating one or more hidden layers between the input and output layers. Each of these layers comprises a collection of neurons, interconnected by weighted connections that facilitate the network's learning and adaptive capabilities.

In the illustration depicted in multi-layer-perceptrons, we observe a Multi-Layer Perceptron configuration featuring an input layer, two hidden layers, and an output layer.

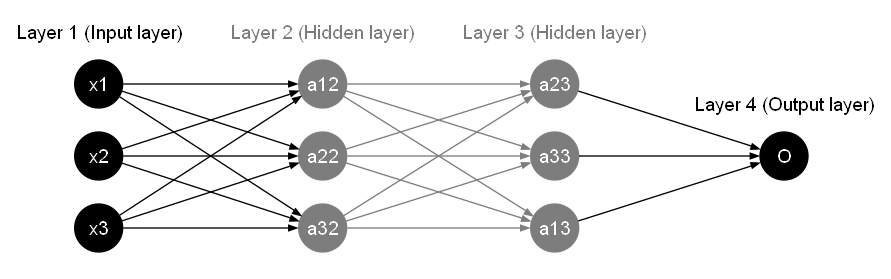
The Multi-Layer Perceptron serves as a foundational concept and a precursor to the modern deep neural networks (DNNs) that have reshaped the field of artificial intelligence. MLP, in its essence, laid the initial groundwork for the development of deep neural networks by introducing the concept of multiple layers of interconnected neurons. MLP gained traction in the 1960s and 1970s as researchers started to explore the capabilities of neural networks beyond the traditional single- layer perceptrons. With MLP, neural networks could now consist of multiple hidden layers, enabling them to model more complex and intricate data representations. While early implementations of MLP struggled with training due to vanishing gradients and limited computational resources, the fundamental idea of stacking multiple layers of neurons to learn hierarchical features remained pivotal.

The key breakthrough came with the development of backpropagation in the 1980s, which allowed for more effective training of MLPs with multiple layers. This innovation, coupled with advances in computing power, laid the groundwork for the resurgence of neural networks in the 21st century. The realization that deeper networks could learn hierarchical representations of data led to the birth of deep learning, where DNNs with numerous hidden layers could autonomously extract complex features from raw data. Today, deep neural networks have transformed various domains, from image and speech recognition to natural language processing and reinforcement learning, underpinning the rapid progress in artificial intelligence and reshaping the technological landscape. In this way, the Multi-Layer Perceptron stands as a pioneering concept that set the stage for the development of the deep neural networks that have become the backbone of modern AI systems.

Architecture of MLPs

The architecture of Multi-Layer Perceptrons (MLPs) consists of multiple layers of interconnected neurons. Each layer serves a specific purpose and contributes to the overall functionality of the network. The key components of an MLP's architecture are as follows:

Input Layer

This is the initial layer that receives the input data, which could be features from a dataset or any other form of input. Each neuron in the input layer corresponds to a feature of the input data. The number of neurons in this layer is determined by the dimensionality of the input data.

The Input Layer serves as the entry point for data into the neural network. Each neuron in this layer corresponds to a specific feature or input variable. The number of neurons in the input layer is determined by the dimensionality of the input data. Input neurons don't perform computations; they merely pass the input data to the subsequent layers.

Hidden Layers

Hidden layers are intermediary layers situated between the input and output layers. They are responsible for transforming the input data through a series of weighted connections and applying activation functions to introduce non-linearity to the network. Hidden layers allow MLPs to capture complex relationships within the data. The number of hidden layers and the number of neurons in each hidden layer are design choices that depend on the complexity of the problem being addressed. Deeper networks with more neurons can model more complex functions but may require more data to train effectively.

Output Layer

The output layer provides the final result of the MLP's computations. The number of neurons in the output layer is determined by the nature of the task the network is performing. For example, in a classification task with multiple classes, there will be one neuron for each class. The output values can represent probabilities or class labels, depending on the specific problem.

Activation Functions

Activation functions are applied to the outputs of neurons in the hidden and output layers. They introduce non-linearity to the network, enabling it to learn complex relationships in the data. Common activation functions include sigmoid, tanh (hyperbolic tangent), and ReLU (Rectified Linear Unit). We will look at some of these activation functions in more detail later in this section.

Neurons and Connections

Neurons in each layer are interconnected with neurons in adjacent layers through weighted connections. Each connection is associated with a weight that determines the strength of the connection. During training, these weights are adjusted to minimize the difference between the predicted output and the actual target values.

Activation Functions

Activation functions are pivotal components within neural networks, transforming the raw input into meaningful outputs. They introduce non-linearity, enabling networks to capture complex relationships and perform intricate tasks.

Commonly used activation functions include the sigmoid function, hyperbolic tangent function, and rectified linear unit (ReLU) function. These functions allow the network to model complex relationships between inputs and outputs, enabling MLPs to solve a wide range of problems.

Let's delve into some of the key activation functions and unveil their mathematical expressions and underlying significance.

Sigmoid Activation Function

The sigmoid activation function addresses the limitations of the step function by producing a continuous output between 0 and 1, which can be interpreted as a probability. The sigmoid function is defined as:

\[ f(x) = \frac{1}{1 + e^{-x}} \]

The sigmoid function's output is smooth and bounded, which aids in gradient-based optimization during training. However, it has a vanishing gradient problem, meaning that as the absolute value of input increases, the gradient approaches zero. This issue can slow down training and make it harder for deep networks to learn complex features.

Hyperbolic Tangent (tanh) Activation Function

The Hyperbolic Tangent, or tanh, function can be described as:

\[ f(x) = \tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \]

Similar to the sigmoid, this function generates an "S"-shaped curve. However, it maps inputs to a range between -1 and 1, placing its midpoint at 0. This property makes it suitable for data encompassing both positive and negative values. The tanh activation function has historically found use in neural networks due to its non-linear behavior while being centered around zero.

Rectified Linear Unit (ReLU) Activation Function

The rectified linear unit, or ReLU, is a widely used activation function that has gained popularity due to its simplicity and effectiveness. It's defined as follows:

\[ f(x) = \max(0, x) \]

In other words, if the input is positive, the ReLU function outputs the input value directly; otherwise, it outputs zero. ReLU overcomes the vanishing gradient problem associated with the sigmoid function because its gradient is either 0 (for negative inputs) or 1 (for positive inputs). This leads to faster convergence during training.

Despite its advantages, ReLU has its own limitations. A phenomenon known as the "dying ReLU" problem can occur when a large portion of the network's neurons output zero during training, effectively preventing those neurons from updating their weights. This issue led to the development of variations like Leaky ReLU and Parametric ReLU, which introduce small gradients for negative inputs, preventing neurons from becoming completely inactive.

Leaky ReLU Activation Function

Leaky ReLU introduces a slight modification to ReLU:

\[ f(x) = \begin{cases} x, & \text{if } x \geq 0 \\ \alpha x, & \text{otherwise} \end{cases} \]

The $\alpha$ value is typically a small positive constant. It is used to introduce a small, positive slope to the function for input values less than zero, preventing neurons from becoming completely inactive when the input is negative.

Leaky ReLU addresses the "dying ReLU" problem where neurons could get stuck during training if they always receive negative inputs, causing them to never update their weights. By introducing a small positive slope, the Leaky ReLU allows gradients to flow backward during training, making it a preferred choice in some neural network architectures.

Exponential Linear Unit (ELU) Activation Function

The Exponential Linear Unit (ELU) activation function is a versatile alternative to rectified linear units (ReLU) that addresses some of the limitations of ReLU. Its mathematical expression is defined as:

\[ f(x) = \begin{cases} x, & \text{if } x \geq 0 \\ a(e^{x} - 1), & \text{otherwise} \end{cases} \]

In above equation, $a$ is a positive constant parameter, which is typically set to a small positive value. This parameter controls the slope of the function for negative inputs.

Here are some advantages of ELU:

Smoothness for Negative Inputs: Unlike ReLU, which abruptly switches off for negative inputs, ELU introduces a smooth, continuous curve for negative values. This smoothness ensures that the activation function and its gradient are always well-defined, even for extreme negative inputs. This characteristic helps mitigate the "dying ReLU" problem, where neurons can become inactive during training due to consistently negative inputs.
Continuous Gradient: The exponential term, $(e^{x} - 1)$, guarantees a continuous gradient for both positive and negative inputs. This is in contrast to ReLU, which has a zero gradient for negative inputs. A continuous gradient aids in faster convergence during training and enhances the overall stability of the optimization process.
Reduced Vanishing Gradient Problem: ELU's continuous gradient also addresses the vanishing gradient problem encountered in deep neural networks. The vanishing gradient problem occurs when gradients become extremely small, hindering the training of deep networks. ELU's gradient is non- zero for all inputs, which helps combat this issue.
Negative Saturation: ELU has a saturation region for negative inputs, which can potentially act as a form of regularization. This can help prevent overfitting by limiting the output of neurons in the negative region, similar to the sigmoid and hyperbolic tangent (tanh) functions.
Enhanced Network Performance: ELU has been shown to improve the performance of deep neural networks in various tasks, including image classification and natural language processing. Its ability to address issues related to training speed and convergence makes it an attractive choice for many deep learning applications.

While ELU offers several advantages, it's essential to consider its computational cost compared to ReLU, especially when dealing with large neural networks. Despite this consideration, ELU has become a popular activation function in the deep learning community due to its ability to alleviate the challenges associated with ReLU while still providing computational efficiency and improved training dynamics.

Scaled Exponential Linear Unit (SELU) Activation Function

The Scaled Exponential Linear Unit (SELU) activation function is a specialized activation function designed to facilitate the self-normalization of neural networks. Its mathematical formulation is defined as:

\[ f(x) = \lambda \begin{cases} x, & \text{if } x \geq 0 \\ \alpha(e^{x} - 1), & \text{otherwise} \end{cases} \]

Here, $\lambda$ and $\alpha$ are constants, typically set to specific values that enable self- normalization. SELU's defining feature is its ability to maintain a stable mean and variance across layers during network training.

Let's explore SELU in more detail:

Self-Normalization: SELU is primarily designed to address the vanishing and exploding gradient problems encountered in deep neural networks. It exhibits a unique self-normalization property, which means that the activations tend to preserve a stable mean and variance as they pass through layers. This self-normalization behavior is particularly advantageous for very deep networks, where maintaining stable gradients is crucial for convergence.
Optimized Training: The self-normalizing property of SELU leads to faster convergence during training. It reduces the need for techniques like batch normalization or careful weight initialization, simplifying the training process and making it more robust.
Adaptation to Complex Data Distributions: SELU's self-normalizing behavior allows neural networks to better adapt to complex data distributions and model intricate relationships in the data. This can result in improved generalization and higher performance on challenging tasks.
Choice of Constants: The values of 'λ' and 'α' are typically set to specific constants that enable self-normalization. The most commonly used values are 'λ = 1.0507' and 'α = 1.67326'. These values are chosen based on mathematical analysis to ensure the self-normalization property.
Practical Applicability: SELU has found success in various deep learning applications, including image recognition, natural language processing, and reinforcement learning. Its ability to accelerate training and enhance network performance has made it an attractive choice for researchers and practitioners in the field.

The Scaled Exponential Linear Unit (SELU) activation function represents a significant advancement in the realm of neural network activation functions. Its self-normalizing property, which helps maintain stable mean and variance across layers, empowers deep neural networks to efficiently handle complex data distributions, leading to faster convergence and improved deep learning capabilities. SELU has become an essential tool in the toolkit of neural network practitioners, contributing to the advancement of artificial intelligence in various domains.

Parametric ReLU (PReLU) Activation Function

Parametric ReLU generalizes the concept of Leaky ReLU: $$ f(x) = \begin{cases} x, & \text{if } x \geq 0 \ a x, & \text{otherwise} \end{cases} $$

Here, $a$ is not a fixed constant like in the Leaky ReLU but is rather a parameter that the neural network learns during the training process. This adaptive nature of $a$ is what sets PReLU apart and allows it to optimize the activation for each neuron individually.

The significance of this adaptability lies in its capacity to improve the model's learning ability. By learning the optimal value of $a$ for each neuron, the network can adjust the slope of the negative part of the activation function as needed. This means that neurons can have varying degrees of leakiness or linearity depending on the characteristics of the data and the specific task at hand.

Here are a few key points to consider about PReLU:

Improved Flexibility: PReLU provides greater flexibility in modeling complex data relationships. By allowing different neurons to have different slopes for their negative parts, it can capture a wider range of patterns and nuances in the data.
Reduced Risk of Dying Neurons: The adaptive 'a' parameter helps mitigate the risk of "dying neurons," where neurons consistently receive negative inputs and never update their weights. With PReLU, even if a neuron has a negative output initially, it can learn to adjust and participate in the learning process.
Regularization Effect: PReLU's learnable parameter 'a' also introduces a form of regularization, as the network must learn the appropriate slope for each neuron. This can prevent overfitting to some extent and improve generalization.
Increased Model Capacity: The adaptive nature of PReLU increases the capacity of the model to approximate complex functions. However, this also means that it might require more data to train effectively and could be more prone to overfitting if not used carefully.

In practice, PReLU has been shown to be particularly useful in deep neural networks, where it can enhance the network's ability to learn hierarchical features and complex data representations. It stands as a powerful tool in the arsenal of activation functions for training deep neural networks.

Learning Algorithms

Training Multi-Layer Perceptrons (MLPs) involves a set of sophisticated algorithms and optimization techniques that enable neural networks to learn from data. One of the foundational algorithms is Backpropagation, which emerged as a breakthrough in the 1980s. Backpropagation is based on the principle of error minimization. It computes the gradient of the network's error (the difference between predicted and actual outputs) with respect to the network's weights and biases. This gradient information guides the adjustments made to the network's parameters using techniques like gradient descent. We will look at backpropagation in detail in the next section.

Gradient Descent is a fundamental optimization method utilized in MLP training. It works by iteratively adjusting the network's weights in the direction of steepest descent of the error surface. This process continues until a minimum or convergence point is reached. To enhance training efficiency, variants like Stochastic Gradient Descent (SGD) and Mini-Batch Gradient Descent are employed. SGD computes gradients and updates weights based on smaller random subsets (mini- batches) of the training data, making it computationally more efficient.

Moreover, advanced optimization techniques like Momentum, Adam, and RMSProp have been developed to accelerate convergence and improve the training process. These methods incorporate concepts such as moving averages of past gradients and adaptive learning rates to navigate the weight space more effectively.